En
este capítulo se
el método llamado análisis
, que se basa principalmente en la aplicación de la ley de Kirchhoff para voltajes (LKV)
alrededor de una trayectoria cerrada. Una trayectoria cerrada se obtiene
empezando en un nodo y regresando al mismo sin pasar por un nodo intermedio más
de una vez. Este análisis
se puede usar en aquellas redes que son planas. Un
plano se distingue, si es
posible dibujar el diagrama del
circuito en una superficie plana de tal forma que ninguna rama quede por debajo
o por encima de ninguna otra rama. Ver figura. 2.8.1a. Como se puede observar
en la figura 2.8.1 b. una red no plana no se puede dibujar sobre una
superficie plana sin, por lo menos una yuxtaposición o cruce entre conductores.
Una
es una propiedad de un
circuito plano y no existe en un circuito no plano. Se define una
como un lazo que no contiene
ningún otro lazo dentro de él. Ver
. 1
La
de malla se define como la
corriente que fluye a través de los
que constituyen la malla. Nótese
que la corriente en un elemento común a dos
es la
algebraica de las
de malla. La corriente de malla
se indica por una flecha
, aunque su dirección es arbitraria es recomendable elegir
siempre corrientes de malla que circulen en el sentido de las manecillas del
, ya que esto ayuda a evitar errores al escribir las ecuaciones resultantes.
Para aclarar esto se puede observar la figura.
2.8.1.2
En
este capítulo se
el método llamado análisis
, que se basa principalmente en la aplicación de la ley de Kirchhoff para voltajes (LKV)
alrededor de una trayectoria cerrada. Una trayectoria cerrada se obtiene
empezando en un nodo y regresando al mismo sin pasar por un nodo intermedio más
de una vez. Este análisis
se puede usar en aquellas redes que son planas. Un
plano se distingue, si es
posible dibujar el diagrama del
circuito en una superficie plana de tal forma que ninguna rama quede por debajo
o por encima de ninguna otra rama. Ver figura. 2.8.1a. Como se puede observar
en la figura 2.8.1 b. una red no plana no se puede dibujar sobre una
superficie plana sin, por lo menos una yuxtaposición o cruce entre conductores.
Una
es una propiedad de un
circuito plano y no existe en un circuito no plano. Se define una
como un lazo que no contiene
ningún otro lazo dentro de él. Ver
. 1
La
de malla se define como la
corriente que fluye a través de los
que constituyen la malla. Nótese
que la corriente en un elemento común a dos
es la
algebraica de las
de malla. La corriente de malla
se indica por una flecha
, aunque su dirección es arbitraria es recomendable elegir
siempre corrientes de malla que circulen en el sentido de las manecillas del
, ya que esto ayuda a evitar errores al escribir las ecuaciones resultantes.
Para aclarar esto se puede observar la figura.
2.8.1.2
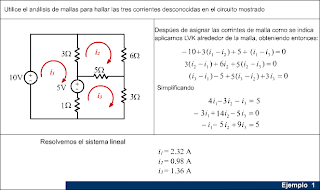
Un circuito que sólo contenga fuentes independientes de voltaje y resistencias, produce un formato específico de ecuaciones que se pueden obtener fácilmente. Ver Ejemplo 1.
Al incorporar fuentes de corriente en los circuitos, el método de análisis sufre un leve cambio, debe tenerse en
cuenta una nueva corriente de malla cuyo valor depende de la magnitud de la fuente incluida que para
este caso es igual al negativo de la fuente de corriente figura. 2.8.2.1.
Se puede escribir:
Sabiendo esto sólo hace falta la primera corriente de malla, por medio de
la LKV se obtiene:
Reemplazando la ec. 2.8.2.1 en la ec. 2.8.2.2 se tiene:
Donde i2=-if son de magnitud conocida.
Suponiendo el
caso en el que se encuentre una fuente de corriente influyendo sobre dos mallas
se puede observar el procedimiento a seguir en el ejemplo
1.
Donde i2=-if son de magnitud conocida.
Otra técnica utilizada cuando se tiene una fuente de corriente común a dos
mallas es la llamada supermalla. Una supermalla es una malla creada a partir de
dos mallas que tienen una fuente de corriente común ya sea dependiente o
independiente, esto significa que se reduce en uno él número de ecuacion.






No hay comentarios:
Publicar un comentario